About Duct Connections
More
About Duct Hose
More
Antistatic Duct Hose for Dry Food
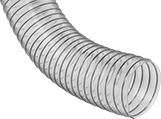
- Flexible
- Compatible Clamps: Worm-Drive Clamps
- Color: Clear
- Temperature Range: -20° to 200° F
Blow grain, sugar, flour, and powders through this hose—it's made of FDA listed materials. Hose has a metal spiral that dissipates static when used in a grounded system. The walls are clear so you can monitor flow.
Spiral | Per Ft. | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | OD | Bend Radius | Compresses To | Max. Vacuum | Max. Pressure | Material Thick. | Interior Surface Texture | Direction | Material | Specifications Met | Surface Resistivity | Max. Continuous Lg., ft. | 1-49 | 50-Up | |
Polyurethane | |||||||||||||||
| 2" | 2 5/16" | 2 1/2" | 50% | 29 in. of Hg @ 72° F | 13 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 000000 | 000000 |
| 2 1/2" | 2 3/4" | 3" | 50% | 29 in. of Hg @ 72° F | 13 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 3" | 3 5/16" | 3 1/2" | 50% | 29 in. of Hg @ 72° F | 12 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 4" | 4 5/16" | 4 1/2" | 50% | 20 in. of Hg @ 72° F | 10 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 5" | 5 5/16" | 5 1/2" | 50% | 15 in. of Hg @ 72° F | 10 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 6" | 6 5/16" | 6 1/2" | 50% | 13 in. of Hg @ 72° F | 9 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 8" | 8 3/8" | 9" | 50% | 10 in. of Hg @ 72° F | 7 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 10" | 10 3/8" | 11 1/2" | 50% | 7 in. of Hg @ 72° F | 5 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
| 12" | 12 3/8" | 13 1/2" | 50% | 6 in. of Hg @ 72° F | 5 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | FDA Compliant 21 CFR 177.2600 | 2 × 1010 ohms/sq. | 50 | 000000 | 00000 | 00000 |
Puncture- and Abrasion-Resistant Duct Hose for Metal Chips and Shavings


- Flexible
- Compatible Clamps: Worm-Drive Clamps
- Color: Clear or Black
- Temperature Range: -65° to 200° F
Blow jagged, abrasive materials through this hose without worrying about punctures or tears. It's made of extra-thick polyurethane.
Clear hose lets you monitor flow.
Warning: Hose should not be used for applications that generate a static charge.
Spiral | Per Ft. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | OD | Bend Radius | Compresses To | Max. Vacuum | Max. Pressure | Material Thick. | Interior Surface Texture | Direction | Material | Max. Continuous Lg., ft. | 1-24 | 25-Up | |
Clear Polyurethane | |||||||||||||
| 2" | 2 5/16" | 2 1/2" | 50% | 29 in. of Hg @ 72° F | 33 psi @ 72° F | 0.035" | Ribbed | Right Hand | Metal | 25 | 0000000 | 000000 | 000000 |
| 2" | 2 5/16" | 3" | 75% | 29 in. of Hg @ 72° F | 35 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 3" | 3 5/16" | 5" | 75% | 29 in. of Hg @ 72° F | 30 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 3" | 3 3/8" | 3 1/2" | 50% | 29 in. of Hg @ 72° F | 27 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 4" | 4 3/8" | 4 1/2" | 50% | 28 in. of Hg @ 72° F | 18 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 4" | 4 7/16" | 4" | 70% | 29 in. of Hg @ 72° F | 35 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 5" | 5 3/8" | 5 1/2" | 50% | 26 in. of Hg @ 72° F | 16 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 5" | 5 7/16" | 5" | 70% | 26 in. of Hg @ 72° F | 31 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 6" | 6 3/8" | 6 1/2" | 50% | 23 in. of Hg @ 72° F | 14 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 6" | 6 7/16" | 6" | 70% | 23 in. of Hg @ 72° F | 27 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 7" | 7 7/16" | 7 1/2" | 50% | 18 in. of Hg @ 72° F | 12 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 7" | 7 1/2" | 7" | 70% | 18 in. of Hg @ 72° F | 26 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 8" | 8 7/16" | 9" | 50% | 13 in. of Hg @ 72° F | 11 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 8" | 8 1/2" | 8" | 70% | 13 in. of Hg @ 72° F | 25 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 10" | 10 7/16" | 11 1/2" | 50% | 6 in. of Hg @ 72° F | 9 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 10" | 10 1/2" | 10" | 70% | 6 in. of Hg @ 72° F | 22 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 12" | 12 7/16" | 13 1/2" | 50% | 5 in. of Hg @ 72° F | 7 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 12" | 12 1/2" | 12" | 70% | 5 in. of Hg @ 72° F | 19 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 14" | 14 9/16" | 15 1/2" | 50% | 3 in. of Hg @ 72° F | 4 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 14" | 14 11/16" | 12" | 70% | 4 in. of Hg @ 72° F | 16 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 16" | 16 5/8" | 18" | 50% | 3 in. of Hg @ 72° F | 2 psi @ 72° F | 0.035" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 16" | 16 11/16" | 12" | 70% | 3 in. of Hg @ 72° F | 13 psi @ 72° F | 0.06" | Ribbed | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
Black Polyurethane | |||||||||||||
| 2" | 2 5/16" | 2" | 30% | 29 in. of Hg @ 72° F | 30 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 3" | 3 5/16" | 3" | 30% | 29 in. of Hg @ 72° F | 29 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 4" | 4 3/8" | 4" | 30% | 29 in. of Hg @ 72° F | 25 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 4" | 4 1/2" | 4" | 50% | 29 in. of Hg @ 72° F | 34 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 5" | 5 5/16" | 5" | 30% | 17 in. of Hg @ 72° F | 22 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 5" | 5 1/2" | 5" | 50% | 17 in. of Hg @ 72° F | 33 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 6" | 6 7/16" | 6" | 30% | 15 in. of Hg @ 72° F | 19 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 6" | 6 1/2" | 6" | 50% | 15 in. of Hg @ 72° F | 32 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 7" | 7 7/16" | 7" | 30% | 12 in. of Hg @ 72° F | 16 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 7" | 7 9/16" | 7" | 50% | 12 in. of Hg @ 72° F | 22 psi @ 72° F | 0.045" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 8" | 8 7/16" | 8" | 30% | 9 in. of Hg @ 72° F | 14 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 8" | 8 9/16" | 8" | 50% | 9 in. of Hg @ 72° F | 29 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 10" | 10 1/2" | 8" | 30% | 4 in. of Hg @ 72° F | 11 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 10" | 10 9/16" | 10" | 50% | 4 in. of Hg @ 72° F | 25 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 12" | 12 1/2" | 10" | 30% | 2.2 in. of Hg @ 72° F | 10 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 12" | 12 9/16" | 12" | 50% | 2.5 in. of Hg @ 72° F | 20 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 14" | 14 9/16" | 12" | 30% | 3.3 in. of Hg @ 72° F | 8 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 14" | 14 5/8" | 14" | 50% | 3.5 in. of Hg @ 72° F | 18 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 16" | 16 9/16" | 14" | 30% | 2.2 in. of Hg @ 72° F | 7 psi @ 72° F | 0.03" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 16" | 16 5/8" | 16" | 50% | 2.5 in. of Hg @ 72° F | 15 psi @ 72° F | 0.06" | Ribbed | Right Hand | Metal | 25 | 0000000 | 000000 | 000000 |
Duct Hose with Wear Strip for Wood Chips and Plastic Pellets
- Flexible
- Color: Clear; Wear Strip is Off-White
- Temperature Range: -20° to 180° F
Not only is polyurethane tough enough to handle heavy particles and cardboard fibers, the material is clear so you can monitor flow. Hose has a wear strip that protects against damage and a copper wire that dissipates static buildup when used in a grounded system.

Spiral | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | OD | Bend Radius | Compresses To | Max. Vacuum | Max. Pressure | Material Thick. | Interior Surface Texture | Direction | Material | Surface Resistivity, ohms/sq. | Max. Continuous Lg., ft. | Per Ft. | |
Per Foot | |||||||||||||
Polyurethane | |||||||||||||
| 1 1/4" | 1 11/16" | 3 1/2" | 70% | 29 in. of Hg @ 72° F | 29 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 0000000 | 00000 |
| 1 1/2" | 1 15/16" | 4" | 70% | 29 in. of Hg @ 72° F | 27 psi @ 72° F | 0.026" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 0000000 | 0000 |
| 1 3/4" | 2 3/16" | 4 1/2" | 70% | 28 in. of Hg @ 72° F | 27 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 0000000 | 0000 |
| 2" | 2 1/2" | 4 1/2" | 70% | 27 in. of Hg @ 72° F | 25 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 0000000 | 0000 |
| 2 1/2" | 3" | 5 1/2" | 70% | 24 in. of Hg @ 72° F | 23 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 0000000 | 00000 |
| 3" | 3 5/8" | 6" | 70% | 20 in. of Hg @ 72° F | 19 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 0000000 | 00000 |
| 4" | 4 5/8" | 7" | 60% | 15 in. of Hg @ 72° F | 9 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 0000000 | 00000 |
| Each | |||||||||||||
Full Coil | |||||||||||||
Polyurethane | |||||||||||||
| 1 1/4" | 1 11/16" | 3 1/2" | 70% | 29 in. of Hg @ 72° F | 29 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 00000000 | 000000 |
| 1 1/2" | 1 15/16" | 4" | 70% | 29 in. of Hg @ 72° F | 27 psi @ 72° F | 0.026" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 00000000 | 000000 |
| 1 3/4" | 2 3/16" | 4 1/2" | 70% | 28 in. of Hg @ 72° F | 27 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 00000000 | 000000 |
| 2" | 2 1/2" | 4 1/2" | 70% | 27 in. of Hg @ 72° F | 25 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 00000000 | 000000 |
| 2 1/2" | 3" | 5 1/2" | 70% | 24 in. of Hg @ 72° F | 23 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 50 | 0000000 | 000000 |
| 3" | 3 5/8" | 6" | 70% | 20 in. of Hg @ 72° F | 19 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 00000000 | 000000 |
| 4" | 4 5/8" | 7" | 60% | 15 in. of Hg @ 72° F | 9 psi @ 72° F | 0.025" | Ribbed | Left Hand | Plastic | 2 × 1010 | 25 | 00000000 | 000000 |

Fittings screw over the end of your duct hose so you can make connections to equipment.
Crush-Resistant Flexible Duct Hose with Wear Strip for Dust


- Flexible
- Compatible Clamps: Worm-Drive and Quick-Release Clamps
- Color: Black or White
- Temperature Range: -60° to 275° F
Surrounded by a protective plastic spiral, this hose bounces back to its original shape when stepped on and resists wear from being dragged across rough floors. Hose has a smooth interior for unrestricted flow. It is often used with lint, dust, and sawdust. It meets UL 94 HB for flame retardance.
Hose that is FDA compliant can be used with dry food, such as flour and sugar.
Warning: Hose should not be used for applications that generate a static charge.
Spiral | Per Ft. | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | OD | Bend Radius | Compresses To | Max. Vacuum | Max. Pressure | Material Thick. | Interior Surface Texture | Direction | Material | Specifications Met | Max. Continuous Lg., ft. | 1-24 | 25-Up | |
Black TPR Rubber | ||||||||||||||
| 3/4" | 13/16" | 1 1/2" | 75% | 29 in. of Hg @ 72° F | 38 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 00000 | 00000 |
| 1" | 1 3/8" | 2 1/2" | 75% | 29 in. of Hg @ 72° F | 34 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 1/4" | 1 11/16" | 2 1/2" | 75% | 29 in. of Hg @ 72° F | 28 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 1/2" | 1 15/16" | 3" | 75% | 29 in. of Hg @ 72° F | 23 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 3/4" | 2 3/16" | 3" | 75% | 29 in. of Hg @ 72° F | 18 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 2" | 2 1/2" | 3 1/2" | 75% | 29 in. of Hg @ 72° F | 17 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 2 1/2" | 3 1/16" | 4" | 75% | 24 in. of Hg @ 72° F | 16 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 3" | 3 9/16" | 5" | 75% | 19 in. of Hg @ 72° F | 14 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 4" | 4 5/8" | 7" | 75% | 16 in. of Hg @ 72° F | 11 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | UL 94 HB | 50 | 0000000 | 00000 | 00000 |
| 6" | 6 11/16" | 7 1/2" | 50% | 10 in. of Hg @ 72° F | 14 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | UL 94 HB | 25 | 0000000 | 00000 | 00000 |
| 8" | 8 7/8" | 9" | 50% | 6 in. of Hg @ 72° F | 14 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | UL 94 HB | 25 | 0000000 | 00000 | 00000 |
| 10" | 10 7/8" | 12" | 50% | 3 in. of Hg @ 72° F | 10 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | UL 94 HB | 25 | 0000000 | 00000 | 00000 |
White TPR Rubber | ||||||||||||||
| 1" | 1 3/8" | 2 1/2" | 75% | 29 in. of Hg @ 72° F | 34 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 1/4" | 1 11/16" | 2 1/2" | 75% | 29 in. of Hg @ 72° F | 28 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 1/2" | 1 15/16" | 3" | 75% | 29 in. of Hg @ 72° F | 23 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 1 3/4" | 2 3/16" | 3" | 75% | 29 in. of Hg @ 72° F | 18 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 2" | 2 1/2" | 3 1/2" | 75% | 29 in. of Hg @ 72° F | 17 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 2 1/2" | 3 1/16" | 4" | 75% | 24 in. of Hg @ 72° F | 16 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 3" | 3 9/16" | 5" | 75% | 19 in. of Hg @ 72° F | 14 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 0000 | 0000 |
| 4" | 4 5/8" | 7" | 75% | 16 in. of Hg @ 72° F | 11 psi @ 72° F | 0.026" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 50 | 0000000 | 00000 | 00000 |
| 6" | 6 11/16" | 7 1/2" | 50% | 10 in. of Hg @ 72° F | 14 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 25 | 0000000 | 00000 | 00000 |
| 8" | 8 7/8" | 9" | 50% | 6 in. of Hg @ 72° F | 14 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 25 | 0000000 | 00000 | 00000 |
| 10" | 10 7/8" | 12" | 50% | 3 in. of Hg @ 72° F | 10 psi @ 72° F | 0.045" | Smooth | Left Hand | Plastic | FDA Compliant 21 CFR 177.2600, UL 94 HB | 25 | 0000000 | 00000 | 00000 |
Abrasion-Resistant Very Flexible Duct Hose for Dust


- Very Flexible
- Compatible Clamps: Worm-Drive Clamps
- Color: Clear or Black
- Temperature Range: -40° to 200° F
A blend of rubber and plastic creates a hose that's flexible, yet tough enough to handle abrasive particles such as grinding dust and sawdust.
Clear hose lets you see what's running through your line. It has a smooth interior for unrestricted flow.
Warning: Hose should not be used for applications that generate a static charge.
Spiral | Per Ft. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ID | OD | Bend Radius | Compresses To | Max. Vacuum | Max. Pressure | Material Thick. | Interior Surface Texture | Direction | Material | Max. Continuous Lg., ft. | 1-24 | 25-Up | |
Clear Polyurethane | |||||||||||||
| 1" | 1 3/8" | 1" | 50% | 28 in. of Hg @ 72° F | 15 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 1 1/4" | 1 5/8" | 1 1/2" | 50% | 28 in. of Hg @ 72° F | 13 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 1 1/2" | 1 7/8" | 1 1/2" | 50% | 26 in. of Hg @ 72° F | 10 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 2" | 2 3/8" | 2" | 50% | 22 in. of Hg @ 72° F | 8 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 2 1/2" | 2 7/8" | 2 1/2" | 50% | 20 in. of Hg @ 72° F | 7 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 3" | 3 3/8" | 3" | 50% | 16 in. of Hg @ 72° F | 6 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 3 1/2" | 3 7/8" | 3" | 55% | 14 in. of Hg @ 72° F | 6 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 00000000 | 0000 | 0000 |
| 4" | 4 3/8" | 4" | 50% | 12 in. of Hg @ 72° F | 5 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 00000 | 0000 |
| 5" | 5 3/8" | 5" | 50% | 10 in. of Hg @ 72° F | 5 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 6" | 6 3/8" | 6" | 50% | 7 in. of Hg @ 72° F | 4 psi @ 72° F | 0.02" | Smooth | Left Hand | Metal | 25 | 0000000 | 00000 | 00000 |
Black Polyurethane | |||||||||||||
| 2" | 2 3/8" | 2" | 35% | 29 in. of Hg @ 72° F | 30 psi @ 72° F | 0.015" | Ribbed | Right Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 2 1/2" | 2 7/8" | 2 1/2" | 25% | 29 in. of Hg @ 72° F | 30 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 0000 | 0000 |
| 3" | 3 3/8" | 3 1/2" | 25% | 29 in. of Hg @ 72° F | 30 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 0000 | 0000 |
| 4" | 4 3/8" | 4" | 25% | 24 in. of Hg @ 72° F | 22 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 0000 |
| 5" | 5 3/8" | 4 1/2" | 25% | 13 in. of Hg @ 72° F | 18 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 6" | 6 3/8" | 5 1/2" | 25% | 8 in. of Hg @ 72° F | 15 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 7" | 7 3/8" | 6" | 20% | 8 in. of Hg @ 72° F | 10 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 8" | 8 3/8" | 6 1/2" | 20% | 2 in. of Hg @ 72° F | 7 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 00000000 | 00000 | 00000 |
| 10" | 10 3/8" | 7 1/2" | 20% | 2 in. of Hg @ 72° F | 7 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 12" | 12 3/8" | 9" | 20% | 1.7 in. of Hg @ 72° F | 6 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 14" | 14 3/8" | 12" | 20% | 1.1 in. of Hg @ 72° F | 5 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 16" | 16 3/8" | 14" | 20% | 0.7 in. of Hg @ 72° F | 5 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |
| 18" | 18 3/8" | 16" | 20% | 0.5 in. of Hg @ 72° F | 4 psi @ 72° F | 0.02" | Ribbed | Right Hand | Metal | 25 | 0000000 | 00000 | 00000 |